该比赛已结束，您无法在比赛模式下递交该题目。您可以点击“在题库中打开”以普通模式查看和递交本题。

题目描述

一幅图画可以表示为一个 $n \times m$ 的网格（$n$ 行 $m$ 列），其中每个格子都被涂上一种颜色。现在你有 $k$ 种不同的颜料，第 $i$ 种颜料最多可以涂 $a_i$ 个格子。

一幅图画被认为是美丽的，当且仅当每个格子都至少有 $3$ 个环形相邻的同色格子。

两个格子被称为环形相邻，如果它们在环形意义下共享一条边。具体来说，对于坐标 $(x_1,y_1)$ 和 $(x_2,y_2)$，当满足以下任一条件时互为环形邻居：

1. $x_1-x_2 \equiv \pm1 \pmod{n}$ 且 $y_1=y_2$（上下相邻）
2. $y_1-y_2 \equiv \pm1 \pmod{m}$ 且 $x_1=x_2$（左右相邻）

每个格子都有恰好 $4$ 个环形相邻的格子。例如在 $3 \times 4$ 的网格中，格子 $(1,2)$ 的环形邻居是 $(3,2)$、$(2,2)$、$(1,3)$ 和 $(1,1)$，如下图所示：

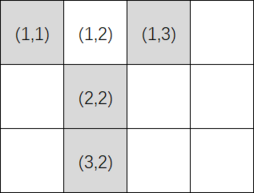
灰色格子表示 $(1,2)$ 的环形邻居

输入格式

• 第一行：整数 $t$（$1 \leq t \leq 10^4$）表示测试用例数量
• 每个测试用例：
  • 第一行：三个整数 $n,m,k$（$1 \leq n,m,k \leq 10^9$）
  • 第二行：$k$ 个整数 $a_1,a_2,...,a_k$（$1 \leq a_i \leq 10^9$）

输出格式

对于每个测试用例，输出一行：

• 如果可以创建美丽图画，输出 "Yes"
• 否则输出 "No"

示例

输入样例

3
2 3 2
3 3
3 3 2
2 2
4 4 1
16

输出样例

No
No
Yes

数据范围

• $1 \leq t \leq 10^4$
• $1 \leq n,m,k \leq 10^9$
• $1 \leq a_i \leq 10^9$
• 所有测试用例的 $k$ 之和不超过 $10^5$

说明

1. 第一个样例可以通过将网格分成两个颜色区域满足条件
2. 第二个样例无法满足每个格子有3个同色邻居的要求
3. 第三个样例可以用单一颜色涂满整个网格